Elliptic Curve arithmetic

The python-ecdsa also provides generic API for performing operations on elliptic curve points.

Warning

This is documentation of a very low-level API, if you want to handle keys or signatures you should look at documentation of the keys module.

Short Weierstrass curves

There are two low-level implementations for short Weierstrass curves: Point and PointJacobi.

Both of them use the curves specified using the CurveFp object.

You can either provide your own curve parameters or use one of the predefined curves. For example, to define a curve 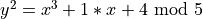$y^2 = x^3 + 1 * x + 4 \text{ mod } 5$ use code like this:

from ecdsa.ellipticcurve import CurveFp
custom_curve = CurveFp(5, 1, 4)

The predefined curves are specified in the ecdsa module, but it’s much easier to use the helper functions (and proper names) from the curves module.

For example, to get the curve parameters for the NIST P-256 curve use this code:

from ecdsa.curves import NIST256p
curve = NIST256p.curve

Tip

You can also use Curve to get the curve parameters from a PEM or DER file. You can also use curve_by_name() to get a curve by specifying its name. Or use the find_curve() to get a curve by specifying its ASN.1 object identifier (OID).

Affine coordinates

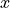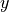After taking hold of curve parameters you can create a point on the curve. The Point uses affine coordinates, i.e. the $x$ and $y$ from the curve equation directly.

To specify a point (1, 1) on the custom_curve you can use this code:

from ecdsa.ellipticcurve import Point
point_a = Point(custom_curve, 1, 1)

Then it’s possible to either perform scalar multiplication:

point_b = point_a * 3

Or specify other points and perform addition:

point_b = Point(custom_curve, 3, 2)
point_c = point_a + point_b

To get the affine coordinates of the point, call the x() and y() methods of the object:

print("x: {0}, y: {1}".format(point_c.x(), point_c.y()))

Projective coordinates

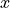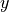When using the Jacobi coordinates, the point is defined by 3 integers, which are related to the $x$ and $y$ in the following way:

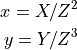
$x = X/Z^2 \\ y = Y/Z^3$

That means that if you have point in affine coordinates, it’s possible to convert them to Jacobi by simply assuming 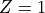$Z = 1$ .

So the same points can be specified as so:

from ecdsa.ellipticcurve import PointJacobi
point_a = PointJacobi(custom_curve, 1, 1, 1)
point_b = PointJacobi(custom_curve, 3, 2, 1)

Note

Unlike the Point, the PointJacobi does not check if the coordinates specify a valid point on the curve as that operation is computationally expensive for Jacobi coordinates. If you want to verify if they specify a valid point, you need to convert the point to affine coordinates and use the contains_point() method.

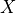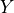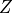Then all the operations work exactly the same as with regular Point implementation. While it’s not possible to get the internal $X$ , $Y$ , and $Z$ coordinates, it’s possible to get the affine projection just like with the regular implementation:

point_c = point_a + point_b
print("x: {0}, y: {1}".format(point_c.x(), point_c.y()))

All the other operations, like scalar multiplication or point addition work on projective points the same as with affine representation, but they are much more effective computationally.